Arjen tilastotiedettä - Myyntiharjoittelijan palkkaaminen

Datatiede-kategorian blogeissa analysoidaan todelliseen elämään pohjautuvia pulmia, joita voidaan ratkoa datan ja tilastojen avulla.

Myyjien arviointi

Olet palkannut viisi uutta myyntiharjoittelijaa, joilla suoritetaan 100 myyntipuhelun mittainen testi. Tiedetään, että harjoittelijoiden tekemien kauppojen keskiarvo 100 puhelun testissä on aiemmin ollut 10.

Testijakson jälkeen varmasti alle keskiverto myyjät halutaan potkita pois, keskinkertaiset saavat uuden mahdollisuuden ja taatusti keskivertoa paremmat palkataan välittömästi.

Näin monta kauppaa uudet harjoittelijat tekivät:

• Kyllikki 17
• Emil 14
• Annika 10
• Lars-Adolf 6
• Sofia 4

Ketkä harjoittelijoista ansaitsevat mahdollisuuden?

Ketkä harjoittelijoista potkitaan pois, ketkä saavat uuden mahdollisuuden ja kenet palkataan varmasti?

Menetelmä parhaiden myyjien tunnistamiseksi

Helpointa olisi tietysti valita mututuntumalla rajat, joiden mukaan henkilöt valitaan tiettyyn ryhmään, mutta silloin kaikki on pelkkää arvailua.

Niin sanotulla khii-neliö (chi-squared) testi on tarkoitettu satunnaisten tapahtumien poissulkemiseen. Sen avulla voidaan esimerkiksi määrittää, ovatko nopanheitot tietyllä todennäköisyydellä satunnaisia, vai eivät. Mikäli heitot eivät vaikuta satunnaisilta, on noppa mahdollisesti painotettu.

Harjoittelijaongelman ratkaisemiskesi uusien harjoittelijoiden suoriutumista verrataan edellisten harjoittelijoiden keskiarvoon. Mikäli voidaan riittävällä varmuudella todeta, että harjoittelijan hyvä tai huono tulos johtui sattumasta, hän pääsee uuteen testiin. Voihan jollakin olla takana huonot yöunet samalla, kun toisen aamukahvissa on ollut vähän tiukemmat purut paremman suorituksen aikaansaamiseksi.

Yksi myyntiharjoittelija yli muiden

Tilastollisen testin tuloksista nähdään, että yksi harjoittelija kannattaa palkata, yksi potkia pois ja kolmea testata lisää.

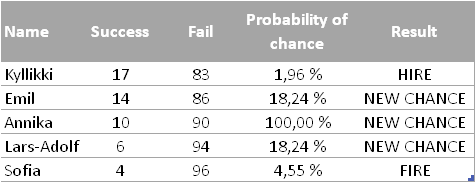
Yllättävää on kuitenkin se, että Emilin ja Lars-Adolfin tulokset näyttävät ensisilmäyksellä olevan selkeästi keskiarvosta poikkeavia. Kun tilastollisen merkitsevyyden raja asetetaan yleisesti käytettyyn viiteen prosenttiin, voidaan todeta, että tulokset menevät tässä tapauksessa satunnaisvaihtelun piikkiin ja heitä kannattaa testata lisää varmuuden saamiseksi.

Tilastollinen perustelu

Tarkoituksena ei ole käydä toteutetun tilastollisentestin teoriaa kokonaan läpi, joten annan esimerkin, kuinka chi-testi tehdään. Lasketaan, mikä on todennäköisyys sille, että Kyllikin oikea taitotaso olisi 10 kauppaa, mutta hän oli onnekas ja saikin nyt 17 kauppaa.

Kaupanteossa on kaksi mahdollista tulosta: kauppa tai ei kauppaa. Kun mahdollisten tulosten määrästä vähennetään yksi, saadaan vapausasteiden määrä. 2-1=1.

Lasketaan seuraavaksi Kyllikin chi-arvo: (17-10)2 / 10 + (83-90)2 / 10 = 5,4444

Tämä arvo ei itsessään kerro mitään. Sen voi ajatella apuarvoksi, jonka merkitys vaihtelee vapausasteen mukaan. Vapausasteen ja saadun arvon antaman todennäköisyyden voi haarukoida taulukosta , mutta helpompaa on käyttää taulukkolaskentaohjelmaa tai ohjelmistoa, jolla vastauksen saa sukkelasti. Chi-arvolla 5,4444 ja vapausasteella 1 vastaukseksi paukahtaa 1,96 %. Luku tarkoittaa sitä, että Kyllikki on keskivertomyyjän tasolla vajaan kahden prosentin todennäköisyydellä.

Excel

=CHISQ.DIST(5,4444;1;TRUE)

R

chi-test.txt Kopioi tiedoston sisältö .R-tiedostoon

#HOW TO USE
#Execute the script and call trainee() function from console

#MASS library is needed for chi square
require(MASS)
library(MASS)

#Create function called "trainee"
trainee <- function(){

  #Get observed successful sales attempts and convert to integer
  obs\_s <- readline(prompt="Successfull attemmpts from 100: ")
  obs\_s <- strtoi(obs\_s)
  #Calculate observed failed sales attempts
  obs\_f <- 100 - obs\_s
  #Create a vector for expected values
  obs <- c(obs\_f,obs\_s)
  
  #Create a vector for expected probabilities
  exp <- c(0.9,0.1)
  
  #Do the chi-test
  test <- chisq.test(obs,p=exp)
  
  #Print p-value
  cat("Probability of chance: ",test$p.value,"\n")
  
  #Probability is stored in test$p.value
  #HIRE if a person is better than the average with 95% confidence
  #FIRE if a person is worse than the average with 95% confidence
  #ELSE give a new chance
  
  #Determine the level of significance to 5%
  sl <- 1-0.95
  
  #Probability is significant and has more than average calls
  if(test$p.value<sl & obs\_s>10){
    cat("HIRE")
  #Significant with less than average calls
  }else if(test$p.value<sl & obs\_s<10){
    cat("FIRE")
  #No significance
  }else{
    cat("NEW CHANCE")
  }
  
}

Tästä pääset videoon , jossa ratkaistaan, onko kolikonheittoje tulos sattumaa vai huijausta.